
Here we will learn about direct proportion, including what direct proportion is and how to solve direct proportion problems. We will also look at solving word problems involving direct proportion.
There are also direct proportion worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
Direct proportion is a type of proportionality relationship. For direct proportion, as one value increases, so does the other value and conversely, as one value decreases, so does the other value.
The symbol \textbf represents a proportional relationship.
If y is directly proportional to x, we can write this relationship as:
Direct proportion is useful in numerous real life situations such as exchange rates, conversion between units, and fuel prices.

The direct proportion formula allows us to express the relationship between two variables, using an equivalence relationship; the formula contains an equals symbol (=) instead of the proportionality symbol (\propto).
When y is directly proportional to x, the value of y \div x is a constant value. This is known as the constant of proportionality and we use the letter k to denote this number.
Given that k=y\div, we can rearrange this formula to make y the subject, and hence obtain the standard format of the direct proportion formula:
Proportional relationships can also be represented graphically.
If we sketched the straight line graph for the equation y=kx, the line must go through the origin (0,0) as the value of the y -intercept is 0, and the gradient of the line is equal to the value of k.
Step-by-step guide: y=mx+c.
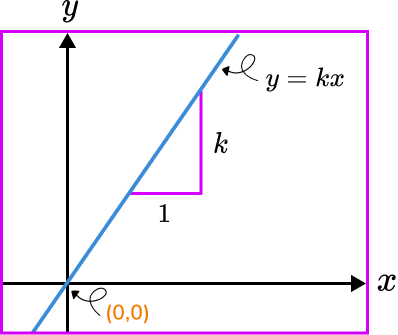
Note, the value of y can be proportional to other powers of x including x^, x^, or even \sqrt. Each of these has a different algebraic and graphical representation.
In order to work out an unknown value given a directly proportional relationship:


Get your free direct proportion worksheet of 20+ questions and answers. Includes reasoning and applied questions.


Get your free direct proportion worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Given that y is directly proportional to x, calculate the value for y when x=6.

As y \propto x we can state the formula y=kx.
2 Determine the value of \textbf .
From the table, we can see that when x=2, y=5. By substituting these values into the formula, we get the value of k.
3 Substitute \textbf and the known value into the direct proportion formula.
Substituting k=2.5 into the formula, we have:
To find the value for y when x=6, substituting x=6 into the equation, we have
4 Solve the equation.
Let y\propto. Calculate the value for x when y=32.

Write down the direct proportion formula.
As y\propto, we can state the formula y=kx.
Determine the value of \textbf .
The constant of proportionality cannot be calculated at the point (0,0) as by substituting this into the formula, we have k=0 \div 0 which is not mathematically possible as we cannot divide by 0.
We therefore have to use the other coordinate (5,8) and substitute these values into y=kx to calculate k.
Substitute \textbf and the known value into the direct proportion formula.
We now have y=1.6x . Substituting y=32 into the equation, we can calculate the value for x:
Solve the equation.
\begin 32&=1.6\times\\\\ 32&=x\times\\\\ 32\div&=x\\\\ x&=20 \endLet y be directly proportional to x^2. Calculate the missing value p.

Write down the direct proportion formula.
We are now given the relationship that y\propto^. This means that the constant of proportionality k=y\div^. Rearranging this formula by multiplying both sides by x^, we get:
Determine the value of \textbf .
We can use either of the two coordinates (2,12) or (3,27) to find k as we know the values for x and y for each point.
Substituting (2,12) into y=kx^2, we have
\begin 12&=k \times 2^2 \\\\ 12&=k \times 4 \\\\ 12 \div 4 &=k \\\\ k&=3 \end
Substitute \textbf and the known value into the direct proportion formula.
As k=3, the direct proportion formula can be written as y=3x^.
When x=4 and y=p , we have
Solve the equation.
\begin p&=3\times\\\\ p&=48 \endA florist uses ribbon to trim bunches of flowers.
80 \ cm of ribbon is needed to make the trimmings on 2 bunches of flowers.
The florist has 9 bunches of flowers to trim today.
How much ribbon will be needed?
Write down the direct proportion formula.
As each bunch of flowers requires a specific length of ribbon, the length of ribbon required (r) is directly proportional to the number of bunches of flowers (b).
Writing this relationship between r and b, we have r \propto b.
This means our direct proportion formula is r=kb where k represents the constant of proportionality.
Determine the value of \textbf .
We currently know that 80cm of ribbon is needed to trim 2 bunches of flowers. This means that when r=80, \ b=2. Substituting these values into the above formula, we have:
Substitute \textbf and the known value into the direct proportion formula.
Now, r=40b. As we need to find out how much ribbon is needed for 9 bunches of flowers, we substitute b=9 into the formula to get:
Solve the equation.
\begin r&=40\times\\\\ r&=360\text \endThe surface area A of a cube is directly proportional to the square of the side length L. A cube with side length 3cm has a surface area of 54cm^.
Determine the side length of a cube with a surface area of 600cm^.
Write down the direct proportion formula.
As A is directly proportional to L^2, we can state that A \propto L^2 and write the formula:
Determine the value of \textbf .
In the question, when A=54, \ L=3. Substituting these values into the formula, we have
Substitute \textbf and the known value into the direct proportion formula.
We have A=6L^. We need to calculate the side length L when the surface area A=600. Substituting these into the formula, we have:
Solve the equation.
\begin 600&=6\times^\\\\ 600\div&=L^\\\\ L^&=100\\\\ L&=\sqrt\\\\ L&=10\text \endLet D represent the density of an object, and V=x^3 represent the volume of the object in terms of the side length x. A block of ice has a density of 0.9g/cm^3 and a volume of 10.8cm^.
Given that D \propto V, determine the side length of a block of ice with the same mass, but a density of 0.92g/cm^. Write your answer to 2 decimal places.
Write down the direct proportion formula.
As D\propto where V=x^3 we can state the direct proportion formula D=kV.
Determine the value of \textbf .
As D=0.9 when V=10.8, substituting these into the formula above, we have
Substitute \textbf and the known value into the direct proportion formula.
We now have D=\fracV. As we want to determine the side length of the new block of ice and V=x^, we can substitute this into the equation, along with the known density D=0.92. We therefore have the following:
Solve the equation.
\begin 0.92\times&=x^\\\\ x^&=11.04\\\\ x&=\sqrt[3]\\\\ x&=2.226672563…\\\\ x&=2.23\text \endIf we represented the direct proportion formula y=kx using a graph, the line would be straight, going through the origin with gradient k. There are many nonlinear direct proportion relationships such as y=kx^2 (a quadratic graph), y=kx^3 (a cubic graph), or y= \sqrt (a radical graph).
These are nonlinear functions as each graph is not a straight line, but x and y are still directly proportional to one another.
Take the general equation of a straight line y=mx+c. The values of x and y are directly proportional if and only if c=0 as the gradient m describes the rate of change between the two variables ( m could be described as the constant of proportionality here). If c ≠ 0, the two variables are not directly proportional.
When using a table, the next value along for x is 3 more than the current value. The value for y is calculated by adding 3 to this value. This uses a summative relationship, rather than the required multiplicative relationship between two variables (the multiplier being the constant of proportionality, k ).
For direct proportion, the constant of proportionality k is the ratio of the two variables such as k=y \div x. For inverse proportion, k is the product of the two variables, such as k=xy.
Step-by-step guide: Inverse proportion (coming soon)
Money is used in many direct proportion word problems. If an answer is 5.3 you may be tempted to write it as £5.3, but the correct way of writing it would be £5.30.
Direct proportion is part of our series of lessons to support revision on proportion. You may find it helpful to start with the main proportion lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
1. y is directly proportional to x. Find the missing value.